Introduction
Can we shrink neural networks without sacrificing much accuracy? Low-rank factorization is a powerful, often overlooked technique that compresses models by decomposing large weight matrices into smaller components.
In this post, we’ll explain what low-rank factorization is, show how to apply it to a ResNet50 model in PyTorch, and evaluate the trade-offs.
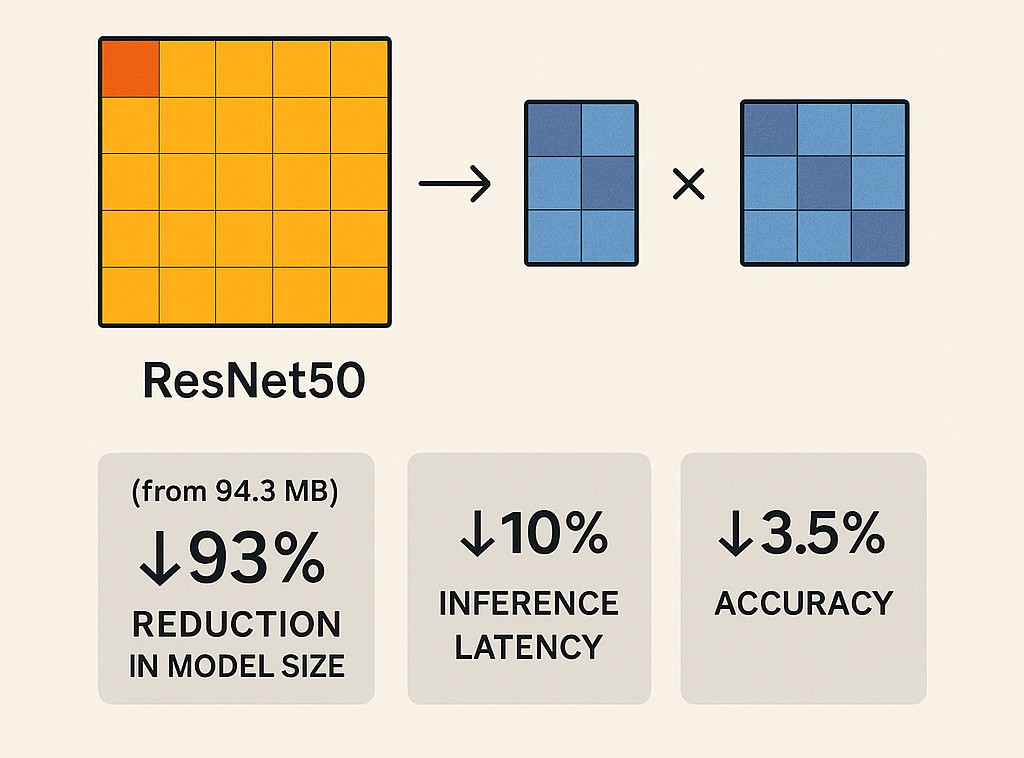
In our example, we achieved a 93% reduction in model size (from 94.38 MB down to 6.9 MB), cut inference latency by 10%, and incurred only a 3.5% drop in accuracy, a compelling trade-off for many practical applications!
What Is Low-Rank Factorization?
Low-rank factorization refers to the process of approximating a matrix with the product of two smaller matrices. If a weight matrix W has shape (m, n) and approximate rank r, we can write:
$$ W ≈ U \cdot V $$ where $$ U ∈ R^{m×r} , V ∈ R^{r×n} $$
This decomposition reduces the number of parameters from m*n to r*(m + n), which is a big win if r << min(m, n).

In deep learning, many weight matrices, especially in linear and convolutional layers, are highly redundant and can be approximated well by low-rank versions. This insight is closely tied to the idea that neural networks overparameterize, and that some of this redundancy can be removed with minimal accuracy loss.
Low-rank factorization is typically achieved by applying Singular Value Decomposition (SVD) to the weight matrix. SVD decomposes a matrix into three components, U, S, and Vᵀ, capturing its principal components. By keeping only the top singular values and corresponding vectors, we can approximate the original matrix with lower rank while preserving most of its information.
However, after factorization, the model usually suffers a drop in accuracy. Fine-tuning the compressed model is typically required to regain most of the original performance.
Where Can We Apply It?
Low-rank factorization is most applicable in the following cases:
-
Fully connected layers: These are easiest to factorize, since their weights are already 2D matrices.
-
Convolutional layers: These need to be reshaped to 2D first (e.g.,
[out_channels, in_channels * kernel_h * kernel_w]), then factored, then reshaped back into two sequential convolutional layers. -
Embedding layers: Can also benefit from factorization in NLP tasks.
It works best on larger layers with high-dimensional weight matrices. You can often skip very small layers or those with strong structural constraints.
Heuristics for where to apply:
- Start with the largest layers, typically toward the end of the model
- Use the SVD spectrum to decide which layers are compressible, a steep drop-off in singular values suggests high redundancy
PyTorch Example: Applying Low-Rank Factorization to ResNet50
In this section, we will apply low-rank factorization to a ResNet50 baseline model, trained on CIFAR-10. We will use various compression ratio to evaluate the accuracy-size-latency trade-offs.
For a complete Jupyter notebook implementation, visit this link. I also added a utils notebook to keep some commonly used functions. Both are part of my Neural Network Optimization GitHub repository.
Training Baseline Model
The code below begins by adapting and training a ResNet50 model on the CIFAR-10 dataset to establish a strong baseline. To maximize the accuracy of both the baseline model and the fine-tuned compressed models, I have enhanced the train function with several advanced features:
- Learning Rate Scheduling: Automatically reduces the learning rate when the validation loss plateaus.
- Early Stopping: Halts training when the validation loss stops improving, preventing overfitting.
- Model Checkpointing: Saves the best-performing model during training for later use.
- Gradient Clipping: Mitigates the risk of exploding gradients by capping the gradient values during backpropagation.
These improvements ensure a robust training process, yielding optimal results for both the original and compressed models.
device = get_device()
train_loader, val_loader, test_loader = get_cifar10_loaders()
model = get_resnet50_for_cifar10(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
criterion = torch.nn.CrossEntropyLoss()
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', patience=3, factor=0.5)
train(
model,
train_loader,
val_loader,
optimizer,
criterion,
device,
epochs=50,
scheduler=scheduler,
grad_clip=1.0,
save_path="full_model_resnet50_best_model.pt",
early_stopping_patience=5,
resume=True,
)
Training Helper Functions
Note: To facilitate reuse and maintain clarity, the commonly used functions have been relocated to a dedicated utils notebook. They are included here for reference and completeness.
def get_device(silent=False):
"""
Returns the device to be used for PyTorch operations.
If a GPU is available, it returns 'cuda', otherwise it returns 'cpu'.
"""
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
if not silent:
print(f"Using device: {device}")
return device
def get_cifar10_loaders(train_ratio=0.9, train_batch_size=128, test_batch_size=128, silent=False):
"""
Returns the CIFAR-10 dataset loaders for training, validation and testing.
The training set is shuffled, while the test set is not.
reference: Learning Multiple Layers of Features from Tiny Images, Alex Krizhevsky, 2009.
"""
# define transform for CIFAR-10 dataset
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean = [0.49139968, 0.48215827, 0.44653124], # CIFAR-10 means
std = [0.24703233, 0.24348505, 0.26158768]) # CIFAR-10 stds
])
# load full CIFAR-10 train set
full_trainset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
# calculate split sizes for train and validation sets
train_size = int(train_ratio * len(full_trainset))
val_size = len(full_trainset) - train_size
# perform split
train_subset, val_subset = random_split(full_trainset, [train_size, val_size])
# create DataLoaders
train_loader = DataLoader(train_subset, batch_size=train_batch_size, shuffle=True)
val_loader = DataLoader(val_subset, batch_size=train_batch_size, shuffle=False)
# CIFAR-10 test set and loader for accuracy evaluation
test_set = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_set, batch_size=test_batch_size, shuffle=False)
if not silent:
print(f"Full train set size: {len(full_trainset)}")
print(f"Train ratio: {train_ratio}")
print(f"Train samples: {len(train_subset)}")
print(f"Validation samples: {len(val_subset)}")
print(f"Test samples: {len(test_set)}")
print(f"Number of training batches: {len(train_loader)}")
print(f"Number of validation batches: {len(val_loader)}")
print(f"Number of test batches: {len(test_loader)}")
return train_loader, val_loader, test_loader
def get_resnet50_for_cifar10(device=None):
"""
Returns a modified ResNet-50 model for CIFAR-10 classification.
"""
if device is None:
device = get_device(silent=True)
model = models.resnet50(weights=None, num_classes=10)
model.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
model.maxpool = nn.Identity()
return model.to(device)
def train(
model,
train_loader,
val_loader,
optimizer,
criterion,
device,
epochs,
scheduler=None,
grad_clip=None,
save_path="best_model.pt",
early_stopping_patience=5,
resume=True
):
"""
Trains the model using the provided data loaders, optimizer, and loss function.
Supports early stopping and model checkpointing.
"""
model.to(device)
start_epoch = 0
best_val_loss = float("inf")
epochs_without_improvement = 0
# Optional resume
if resume and os.path.exists(save_path):
checkpoint = torch.load(save_path, map_location=device)
model.load_state_dict(checkpoint["model_state"])
optimizer.load_state_dict(checkpoint["optimizer_state"])
if "scheduler_state" in checkpoint and scheduler:
scheduler.load_state_dict(checkpoint["scheduler_state"])
best_val_loss = checkpoint.get("best_val_loss", best_val_loss)
start_epoch = checkpoint.get("epoch", 0) + 1
print(f"🔁 Resumed training from epoch {start_epoch}")
for epoch in range(start_epoch, epochs):
model.train()
total_loss = 0.0
total_correct = 0
total_samples = 0
train_loop = tqdm(train_loader, desc=f"[Epoch {epoch+1}/{epochs}]", leave=False)
for inputs, targets in train_loop:
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, targets)
loss.backward()
if grad_clip is not None:
torch.nn.utils.clip_grad_norm_(model.parameters(), grad_clip)
optimizer.step()
total_loss += loss.detach()
preds = outputs.argmax(dim=1)
total_correct += (preds == targets).sum().item()
total_samples += targets.size(0)
avg_train_loss = total_loss / len(train_loader)
train_accuracy = total_correct / total_samples
tqdm.write(f"Epoch {(epoch+1):>3} | Train Loss: {avg_train_loss.item():.4f} | Acc: {train_accuracy:.4f}")
# Validation
model.eval()
val_loss = 0.0
val_correct = 0
val_samples = 0
with torch.no_grad():
for inputs, targets in val_loader:
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
loss = criterion(outputs, targets)
val_loss += loss.detach()
preds = outputs.argmax(dim=1)
val_correct += (preds == targets).sum().item()
val_samples += targets.size(0)
avg_val_loss = val_loss / len(val_loader)
val_accuracy = val_correct / val_samples
tqdm.write(f" | Val Loss: {avg_val_loss.item():.4f} | Acc: {val_accuracy:.4f}")
# Scheduler step
if scheduler is not None:
try:
scheduler.step(avg_val_loss) # for ReduceLROnPlateau
except TypeError:
scheduler.step()
# Early stopping + checkpoint
if avg_val_loss.item() < best_val_loss:
best_val_loss = avg_val_loss.item()
epochs_without_improvement = 0
torch.save({
"model_state": model.state_dict(),
"optimizer_state": optimizer.state_dict(),
"scheduler_state": scheduler.state_dict() if scheduler else None,
"best_val_loss": best_val_loss,
"epoch": epoch,
}, save_path)
tqdm.write(f" | ✅ New best model saved to '{save_path}'")
else:
epochs_without_improvement += 1
tqdm.write(f" | No improvement for {epochs_without_improvement} epoch(s)")
if epochs_without_improvement >= early_stopping_patience:
tqdm.write(f"🛑 Early stopping triggered after {early_stopping_patience} epochs without improvement.")
break
print("Training complete.")
Low-Rank Factorization
Once the baseline model is established, we apply low-rank factorization to compress it. As described earlier, we iterate through all linear and convolutional layers, replacing their weight matrices wherever it results in a meaningful reduction in model size. For linear layers, the weight matrix is factorized into two smaller matrices, which are implemented as two sequential linear layers. For convolutional layers, the weight tensor is first reshaped into a 2D matrix, factorized, and then replaced with two consecutive convolutional layers that approximate the original operation.
It is worth noting that if the reduction in size is not substantial, the latency might slightly increase. This is due to the additional overhead of performing two matrix multiplications instead of the single operation in the original layer. This trade-off is evident in the first few rows of the results table below.
def compress_layer(layer, epsilon=0.10):
"""
Compresses a layer using SVD if the compression is beneficial.
Args:
layer (nn.Module): The layer to compress.
epsilon (float): The energy threshold for compression.
Returns:
nn.Module: The compressed layer or the original layer if compression is not beneficial.
"""
# handle Linear layers
if isinstance(layer, nn.Linear):
# get linear layer weight matrix
W = layer.weight.data.cpu()
# run SVD on flat weight matrix
U, S, Vh = torch.linalg.svd(W, full_matrices=False)
# find rank that capture the asked energy (1-epsilon)
energy = torch.cumsum(S**2, dim=0) / torch.sum(S**2)
rank = torch.searchsorted(energy, 1 - epsilon).item() + 1
# check that factorization actually reduces number of parameters
old_size = W.numel()
new_size = rank * (W.shape[0] + W.shape[1])
if new_size < old_size:
# define low rank factorization from SVD and rank
U_r = U[:, :rank] @ torch.diag(S[:rank])
V_r = Vh[:rank, :]
# define two linear layers to replace the original linear layer
compressed_layer = nn.Sequential(
nn.Linear(W.shape[1], rank, bias=False),
nn.Linear(rank, W.shape[0], bias=True)
)
compressed_layer[0].weight.data = V_r.to(device)
compressed_layer[1].weight.data = U_r.to(device)
compressed_layer[1].bias.data = layer.bias.data.to(device)
return compressed_layer, old_size, new_size
# handle Conv2d layers
elif isinstance(layer, nn.Conv2d):
# get convolution weight 4d matrix, shape: [out_channels, in_channels, kH, kW]
W = layer.weight.data.cpu()
OC, IC, kH, kW = W.shape
# reshape to 2d matrix, with shape: [OC, IC*kH*kW]
W_flat = W.view(OC, -1)
# run SVD on flat weight matrix
U, S, Vh = torch.linalg.svd(W_flat, full_matrices=False)
# find rank that capture the asked energy (1-epsilon)
energy = torch.cumsum(S**2, dim=0) / torch.sum(S**2)
rank = torch.searchsorted(energy, 1 - epsilon).item() + 1
# check that factorization actually reduces number of parameters
old_size = W.numel()
new_size = rank * (IC * kH * kW + OC)
if new_size < old_size:
# define low rank factorization from SVD and rank
U_r = U[:, :rank] @ torch.diag(S[:rank])
V_r = Vh[:rank, :]
# define two convolutional layers to replace the original convolutional layer
conv1 = nn.Conv2d(
in_channels=IC,
out_channels=rank,
kernel_size=1,
stride=1,
padding=0,
bias=False
)
conv2 = nn.Conv2d(
in_channels=rank,
out_channels=OC,
kernel_size=(kH, kW),
stride=layer.stride,
padding=layer.padding,
bias=(layer.bias is not None)
)
conv1.weight.data = V_r.view(rank, IC, kH, kW).to(device)
conv2.weight.data = U_r.view(OC, rank, 1, 1).to(device)
if layer.bias is not None:
conv2.bias.data = layer.bias.data.to(device)
return nn.Sequential(conv1, conv2), old_size, new_size
return layer, 0, 0 # return the original layer if compression is not beneficial
def compress_model(model, epsilon=0.50):
"""
Compresses the given model by applying SVD-based compression to Linear and Conv2d layers.
Args:
model (nn.Module): The model to compress.
epsilon (float): The energy threshold for compression.
Returns:
nn.Module: The compressed model.
"""
compressed_model = deepcopy(model) # Create a copy of the input model
total_old_size = 0
total_new_size = 0
for name, module in compressed_model.named_modules():
if isinstance(module, (nn.Linear, nn.Conv2d)):
if '.' in name: # Check if the module has a parent
parent, attr = name.rsplit('.', 1)
parent_module = compressed_model
for part in parent.split('.'):
parent_module = getattr(parent_module, part)
else: # Handle top-level modules
parent_module = compressed_model
attr = name
new_layer, old_size, new_size = compress_layer(module, epsilon)
total_old_size += old_size
total_new_size += new_size
setattr(parent_module, attr, new_layer)
return compressed_model, total_old_size, total_new_size
Exploring the Impact of Epsilon on Compression and Performance
The low-rank factorization method introduces a hyperparameter, epsilon, which determines the proportion of singular values to trim during compression. The code below explores a range of epsilon values to evaluate the trade-offs between compression gains and performance costs. Each compressed model is fine-tuned to maximize its performance after applying the factorization.
# Evaluate and print metrics for the original model
acc_orig = evaluate(original_model, test_loader, device)
example_input = torch.rand(128, 3, 32, 32).to(device)
orig_latency_mu, orig_latency_std = estimate_latency(original_model, example_input)
size_orig = get_size(original_model)
print(f"Original -> acc: {100*acc_orig:.2f}%, latency: {orig_latency_mu:.2f} ± {orig_latency_std:.2f} ms, size: {size_orig:.2f}MB")
# Iterate over epsilon values
for epsilon in [round(x * 0.1, 2) for x in range(1, 10)]:
print(f"\nCompressing model with epsilon = {epsilon}...")
# Compress the model
compressed_model, total_old_size, total_new_size = compress_model(original_model, epsilon=epsilon)
# Evaluate compressed model before fine-tuning
acc_comp = evaluate(compressed_model, test_loader, device)
print(f"Old size: {total_old_size}, New size: {total_new_size}, Parameter count reduction: {total_old_size-total_new_size}")
print(f"Compressed -> acc before tuning: {100*acc_comp:.2f}%")
# Fine-tune the compressed model
optimizer = torch.optim.Adam(compressed_model.parameters(), lr=1e-3)
criterion = torch.nn.CrossEntropyLoss()
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', patience=2, factor=0.5)
train(
compressed_model,
train_loader,
val_loader,
optimizer,
criterion,
device,
epochs=50,
scheduler=scheduler,
grad_clip=1.0,
save_path=f"compressed_model_epsilon_{epsilon}_best_model.pt",
early_stopping_patience=3,
resume=False,
)
# Evaluate compressed model after fine-tuning
acc_tuned_comp = evaluate(compressed_model, test_loader, device)
comp_latency_mu, comp_latency_std = estimate_latency(compressed_model, example_input)
size_comp = get_size(compressed_model)
# Print metrics for the fine-tuned compressed model
print(f"Compressed -> acc after tuning: {100*acc_tuned_comp:.2f}%, latency: {comp_latency_mu:.2f} ± {comp_latency_std:.2f} ms, size: {size_comp:.2f}MB")
Results
As demonstrated in the table below, selecting the optimal compression ratio allowed us to achieve a remarkable 93% reduction in network size, shrinking it from 94.38 MB to just 6.9 MB. Additionally, we observed a 10% decrease in latency, all while incurring only a modest 3.5% drop in accuracy, a highly favorable trade-off for many practical applications.
| Model | Accuracy | Latency (ms) | Size (MB) | Size Reduction |
|---|---|---|---|---|
| Baseline | 84.64 % | 71.87 ms | 94.38 MB | |
| Compressed, eps=0.10 | 80.78 % | 84.57 ms | 69.86 MB | -26 % |
| Compressed, eps=0.20 | 80.18 % | 78.12 ms | 45.37 MB | -52 % |
| Compressed, eps=0.30 | 81.17 % | 70.42 ms | 28.74 MB | -70 % |
| Compressed, eps=0.40 | 79.75 % | 68.78 ms | 17.93 MB | -81 % |
| Compressed, eps=0.50 | 78.98 % | 65.52 ms | 11.14 MB | -88 % |
| Compressed, eps=0.60 | 81.14 % | 64.47 ms | 6.90 MB | -93 % |
| Compressed, eps=0.70 | 75.46 % | 64.04 ms | 4.16 MB | -96 % |
| Compressed, eps=0.80 | 68.11 % | 63.51 ms | 2.46 MB | -97 % |
| Compressed, eps=0.90 | 35.11 % | 66.13 ms | 1.37 MB | -98 % |
When It Works, and When It Doesn’t
Low-rank factorization is especially effective when:
- You’re working with large layers
- You can tolerate a small accuracy drop
- Deployment constraints favor smaller or faster models
It’s less useful when:
- The network is already compact
- Most layers are small or already optimized
- You’re applying it blindly without analyzing the rank spectrum
It’s important to validate the impact layer by layer. Not every matrix benefits from rank reduction.
Combining with Other Techniques
Low-rank factorization plays well with other compression techniques:
- Pruning: Prune weights before or after factorization for even more savings.
- Quantization: Factor the model, then apply INT8 quantization to further shrink.
- Knowledge Distillation: Use a distilled model as the starting point for factorization, better performance and fewer parameters.
In some settings, stacking these methods leads to additive gains with only minimal engineering overhead.
Summary
Low-rank factorization is a matrix decomposition technique that reduces the size of neural networks by approximating weight matrices with fewer parameters. This method is particularly effective for compressing large, redundant layers, achieving significant reductions in model size and latency with minimal accuracy loss when fine-tuned. By leveraging Singular Value Decomposition (SVD), it simplifies implementation and can be combined with other optimization techniques like pruning, quantization, and knowledge distillation for even greater efficiency. This post demonstrated its application on a ResNet50 model, achieving a 93% size reduction and a 10% latency improvement with only a 3.5% accuracy drop, showcasing its practicality for real-world deployments.